Distance to nearest neighbor¶
Estimating the optimal distance threshold for partitioning clonally related sequences is accomplished by calculating the distance from each sequence in the data set to its nearest neighbor and finding the break point in the resulting bi-modal distribution that separates clonally related from unrelated sequences. This is done via the following steps:
- Calculating of the nearest neighbor distances for each sequence.
- Generating a histogram of the nearest neighbor distances followed by either manual inspect for the threshold separating the two modes or automated threshold detection.
Example data¶
A small example AIRR Rearrangement database is included in the
alakazam package. Calculating the nearest neighbor distances requires
the following fields (columns) to be present in the table:
sequence_idv_callj_calljunctionjunction_length
# Import required packages
library(alakazam)
library(dplyr)
library(ggplot2)
library(shazam)
# Load and subset example data (for speed)
data(ExampleDb, package="alakazam")
set.seed(112)
db <- ExampleDb %>% sample_n(size=500)
db %>% count(sample_id)
## # A tibble: 2 × 2
## sample_id n
## <chr> <int>
## 1 +7d 253
## 2 -1h 247
Calculating nearest neighbor distances (heavy chain sequences)¶
By default, distToNearest, the function for calculating distance
between every sequence and its nearest neighbor, assumes that it is
running under non-single-cell mode and that every input sequence is a
heavy chain sequence and will be used for calculation. It takes a few
parameters to adjust how the distance is measured.
- If a genotype has been inferred using the methods in the
tiggerpackage, and av_call_genotypedfield has been added to the database, then this column may be used instead of the defaultv_callcolumn by specifying thevCallColumnargument.- This will allows the more accurate V call from
tiggerto be used for grouping of the sequences. - Furthermore, for more leniency toward ambiguous V(D)J segment
calls, the parameter
firstcan be set toFALSE. - Setting
first=FALSEwill use the union of all possible genes to group sequences, rather than the first gene in the field.
- This will allows the more accurate V call from
- The
modelparameter determines which underlying SHM model is used to calculate the distance.- The default model is single nucleotide Hamming distance with
gaps considered as a match to any nucleotide (
ham). - Other options include a human Ig-specific single nucleotide
model similar to a transition/transversion model (
hh_s1f) and the corresponding 5-mer context model from Yaari et al, 2013 (hh_s5f), an analogous pair of mouse specific models from Cui et al, 2016 (mk_rs1nfandmk_rs5nf), and amino acid Hamming distance (aa).
- The default model is single nucleotide Hamming distance with
gaps considered as a match to any nucleotide (
Note: Human and mouse distance measures that are backward compatible
with SHazaM v0.1.4 and Change-O v0.3.3 are also provided as
hs1f_compat and m1n_compat, respectively.
For models that are not symmetric (e.g., distance from A to B is not
equal to the distance from B to A), there is a symmetry parameter that
allows the user to specify whether the average or minimum of the two
distances is used to determine the overall distance.
# Use nucleotide Hamming distance and normalize by junction length
dist_ham <- distToNearest(db %>% filter(sample_id == "+7d"),
sequenceColumn="junction",
vCallColumn="v_call_genotyped", jCallColumn="j_call",
model="ham", normalize="len", nproc=1)
# Use genotyped V assignments, a 5-mer model and no normalization
dist_s5f <- distToNearest(db %>% filter(sample_id == "+7d"),
sequenceColumn="junction",
vCallColumn="v_call_genotyped", jCallColumn="j_call",
model="hh_s5f", normalize="none", nproc=1)
Calculating nearest neighbor distances (single-cell paired heavy and light chain sequences)¶
The distToNearest function also supports running under single-cell
mode where an input Example10x containing single-cell paired
IGH:IGK/IGL, TRB:TRA, or TRD:TRG chain sequences are supplied. In this
case, by default, cells are first divided into partitions containing the
same heavy/long chain (IGH, TRB, TRD) V gene and J gene (and if
specified, junction length), and the same light/short chain (IGK, IGL,
TRA, TRG) V gene and J gene (and if specified, junction length). Then,
only the heavy chain sequences are used for calculating the nearest
neighbor distances.
Under the single-cell mode, each row of the input Example10x should
represent a sequence/chain. Sequences/chains from the same cell are
linked by a cell ID in a cellIdColumn column. Note that a cell should
have exactly one IGH sequence (BCR) or TRB/TRD (TCR). The values
in the locusColumn column must be one of IGH, IGI, IGK, or IGL
(BCR) or TRA, TRB, TRD, or TRG (TCR). To invoke the single-cell
mode, cellIdColumn must be specified and locusColumn must be
correct.
There is a choice of whether grouping should be done as a one-stage
process or a two-stage process. This can be specified via VJthenLen.
- In the one-stage process (
VJthenLen=FALSE), cells are divided into partitions containing same heavy/long chain V gene, J gene, and junction length (V-J-length combination), and the same light chain V-J-length combination. - In the two-stage process (
VJthenLen=TRUE), cells are first divided by heavy/long chain V gene and J gene (V-J combination), and light/short chain V-J combination; and then by the corresponding junction lengths.
There is also a choice of whether grouping should be done using IGH
(BCR) or TRB/TRD (TCR) sequences only, or using both IGH and
IGK/IGL (BCR) or TRB/TRD and TRA/TRG (TCR) sequences. This
is governed by onlyHeavy.
# Single-cell mode
# Group cells in a one-stage process (VJthenLen=FALSE) and using
# both heavy and light chain sequences (onlyHeavy=FALSE)
data(Example10x, package="alakazam")
dist_sc <- distToNearest(Example10x, cellIdColumn="cell_id", locusColumn="locus",
VJthenLen=FALSE, onlyHeavy=FALSE)
Regardless of whether grouping was done using only the heavy chain
sequences, or both heavy and light chain sequences, only heavy chain
sequences will be used for calculating the nearest neighbor distances.
Hence, under the single-cell mode, rows in the returned data.frame
corresponding to light chain sequences will have NA in the
dist_nearest field.
Using nearest neighbor distances to determine clonal assignment thresholds¶
The primary use of the distance to nearest calculation in SHazaM is to
determine the optimal threshold for clonal assignment using the
DefineClones tool in Change-O. Defining a threshold relies on
distinguishing clonally related sequences (represented by sequences with
close neighbors) from singletons (sequences without close neighbors),
which show up as two modes in a nearest neighbor distance histogram.
Thresholds may be manually determined by inspection of the nearest
neighbor histograms or by using one of the automated threshold detection
algorithms provided by the findThreshold function. The available
methods are density (smoothed density) and gmm (gamma/Gaussian
mixture model), and are chosen via the method parameter of
findThreshold.
Threshold determination by manual inspection¶
Manual threshold detection simply involves generating a histrogram for
the values in the dist_nearest column of the distToNearest output
and selecting a suitable value within the valley between the two modes.
# Generate Hamming distance histogram
p1 <- ggplot(subset(dist_ham, !is.na(dist_nearest)),
aes(x=dist_nearest)) +
geom_histogram(color="white", binwidth=0.02) +
geom_vline(xintercept=0.12, color="firebrick", linetype=2) +
labs(x = "Hamming distance", y = "Count") +
scale_x_continuous(breaks=seq(0, 1, 0.1)) +
theme_bw()
plot(p1)
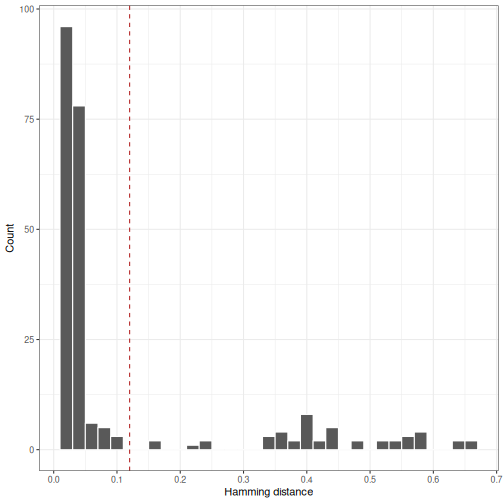
By manual inspection, the length normalized ham model distance
threshold would be set to a value near 0.12 in the above example.
# Generate HH_S5F distance histogram
p2 <- ggplot(subset(dist_s5f, !is.na(dist_nearest)),
aes(x=dist_nearest)) +
geom_histogram(color="white", binwidth=1) +
geom_vline(xintercept=7, color="firebrick", linetype=2) +
labs(x = "HH_S5F distance", y = "Count") +
scale_x_continuous(breaks=seq(0, 50, 5)) +
theme_bw()
plot(p2)
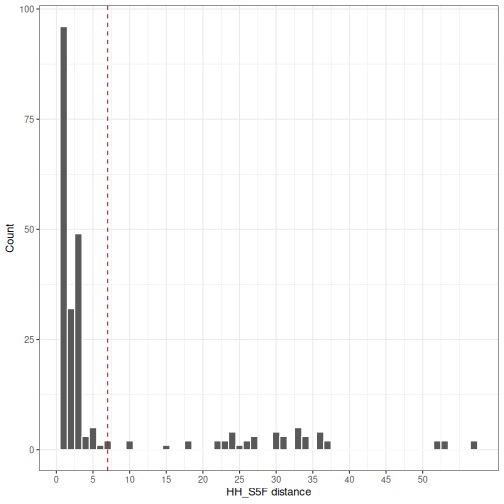
In this example, the unnormalized hh_s5f model distance threshold
would be set to a value near 7.
Automated threshold detection via smoothed density¶
The density method will look for the minimum in the valley between two
modes of a smoothed distribution based on the input vector
(distances), which will generally be the dist_nearest column from
the distToNearest output. Below is an example of using the density
method for threshold detection.
# Find threshold using density method
output <- findThreshold(dist_ham$dist_nearest, method="density")
threshold <- output@threshold
# Plot distance histogram, density estimate and optimum threshold
plot(output, title="Density Method")
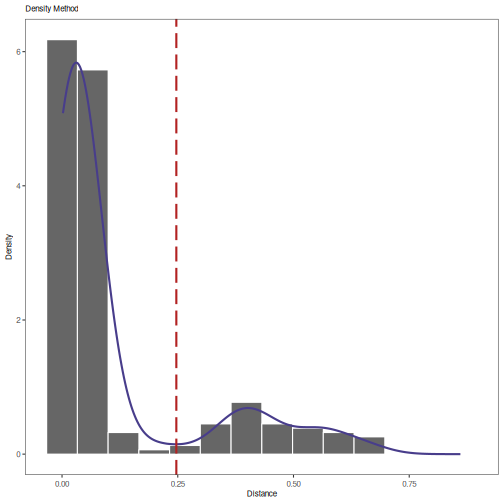
# Print threshold
print(output)
## [1] 0.2468924
Automated threshold detection via a mixture model¶
The findThreshold function includes approaches for automatically
determining a clonal assignment threshold. The "gmm" method
(gamma/Gaussian mixture method) of findThreshold (method="gmm")
performs a maximum-likelihood fitting procedure over the
distance-to-nearest distribution using one of four combinations of
univariate density distribution functions: "norm-norm" (two Gaussian
distributions), "norm-gamma" (lower Gaussian and upper gamma
distribution), "gamma-norm" (lower gamm and upper Gaussian
distribution), and "gamma-gamma" (two gamma distributions). By
default, the threshold will be selected by calculating the distance at
which the average of sensitivity and specificity reaches its maximum
(cutoff="optimal"). Alternative threshold selection criteria are also
providing, including the curve intersection (cutoff="intersect"), user
defined sensitivity (cutoff="user", sen=x), or user defined
specificity (cutoff="user", spc=x)
In the example below the mixture model method (method="gmm") is used
to find the optimal threshold for separating clonally related sequences
by fitting two gamma distributions (model="gamma-gamma"). The red
dashed-line shown in figure below defines the distance where the average
of the sensitivity and specificity reaches its maximum.
# Find threshold using gmm method
output <- findThreshold(dist_ham$dist_nearest, method="gmm", model="gamma-gamma")
# Plot distance histogram, Gaussian fits, and optimum threshold
plot(output, binwidth=0.02, title="GMM Method: gamma-gamma")
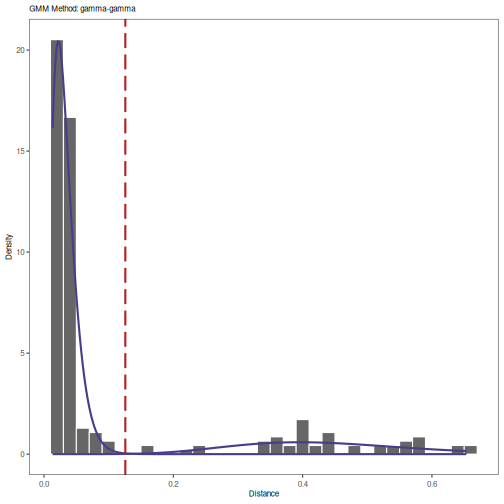
# Print threshold
print(output)
## [1] 0.1257519
Note: The shape of histogram plotted by plotGmmThreshold is
governed by the binwidth parameter. Meaning, any change in bin size
will change the form of the distribution, while the gmm method is
completely bin size independent and only engages the real input data.
Calculating nearest neighbor distances independently for subsets of data¶
The fields argument to distToNearest will split the input
data.frame into groups based on values in the specified fields
(columns) and will treat them independently. For example, if the input
data has multiple samples, then fields="sample_id" would allow each
sample to be analyzed separately.
In the previous examples we used a subset of the original example data.
In the following example, we will use the two available samples, -1h
and +7d, and will set fields="sample_id". This will reproduce
previous results for sample +7d and add results for sample -1d.
dist_fields <- distToNearest(db, model="ham", normalize="len",
fields="sample_id", nproc=1)
We can plot the nearest neighbor distances for the two samples:
# Generate grouped histograms
p4 <- ggplot(subset(dist_fields, !is.na(dist_nearest)),
aes(x=dist_nearest)) +
geom_histogram(color="white", binwidth=0.02) +
geom_vline(xintercept=0.12, color="firebrick", linetype=2) +
labs(x = "Grouped Hamming distance", y = "Count") +
facet_grid(sample_id ~ ., scales="free_y") +
theme_bw()
plot(p4)
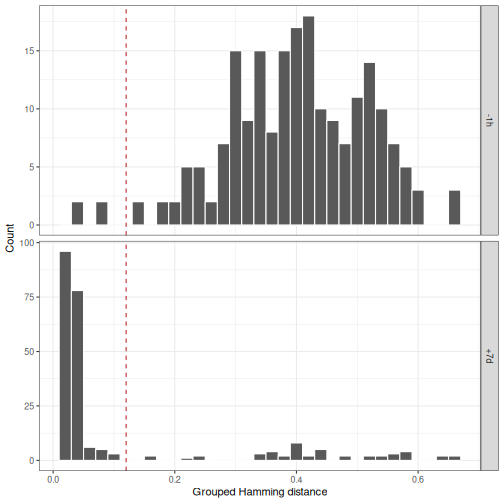
In this case, the threshold selected for +7d seems to work well for
-1d as well.
Calculating nearest neighbor distances across groups rather than within a groups¶
Specifying the cross argument to distToNearest forces distance
calculations to be performed across groups, such that the nearest
neighbor of each sequence will always be a sequence in a different
group. In the following example we set cross="sample", which will
group the data into -1h and +7d sample subsets. Thus, nearest
neighbor distances for sequences in sample -1h will be restricted to
the closest sequence in sample +7d and vice versa.
dist_cross <- distToNearest(ExampleDb, sequenceColumn="junction",
vCallColumn="v_call_genotyped", jCallColumn="j_call",
model="ham", first=FALSE,
normalize="len", cross="sample_id", nproc=1)
# Generate cross sample histograms
p5 <- ggplot(subset(dist_cross, !is.na(cross_dist_nearest)),
aes(x=cross_dist_nearest)) +
labs(x = "Cross-sample Hamming distance", y = "Count") +
geom_histogram(color="white", binwidth=0.02) +
geom_vline(xintercept=0.12, color="firebrick", linetype=2) +
facet_grid(sample_id ~ ., scales="free_y") +
theme_bw()
plot(p5)
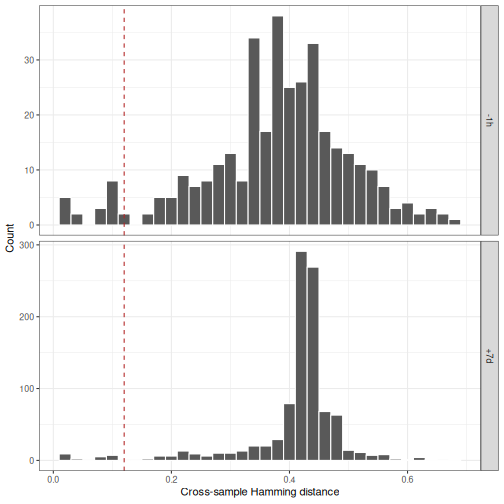
This can provide a sense of overlap between samples or a way to compare within-sample variation to cross-sample variation.
Speeding up pairwise-distance-matrix calculations with subsampling¶
The subsample option in distToNearest allows to speed up
calculations and reduce memory usage.
If there are very large groups of sequences that share V call, J call
and junction length, distToNearest will need a lot of memory and it
will take a long time to calculate all the distances. Without
subsampling, in a large group of n=70,000 sequences distToNearest
calculates a n*n distance matrix. With subsampling, e.g. to s=15,000,
the distance matrix for the same group has size s*n, and for each
sequence in db, the distance value is calculated by comparing the
sequence to the subsampled sequences from the same V-J-junction length
group.
# Explore V-J-junction length groups sizes to use subsample
# Show the size of the largest groups
top_10_sizes <- ExampleDb %>%
group_by(junction_length) %>% # Group by junction length
do(alakazam::groupGenes(., first=TRUE)) %>% # Group by V and J call
mutate(GROUP_ID=paste(junction_length, vj_group, sep="_")) %>% # Create group ids
ungroup() %>%
group_by(GROUP_ID) %>% # Group by GROUP_ID
distinct(junction) %>% # Count unique junctions per group
summarize(SIZE=n()) %>% # Get the size of the group
arrange(desc(SIZE)) %>% # Sort by decreasing size
select(SIZE) %>%
top_n(10) # Filter to the top 10
## Selecting by SIZE
top_10_sizes
## # A tibble: 10 × 1
## SIZE
## <int>
## 1 89
## 2 37
## 3 36
## 4 34
## 5 33
## 6 33
## 7 32
## 8 26
## 9 25
## 10 25
# Use 30 to subsample
# NOTE: This is a toy example. Subsampling to 30 sequence with real data is unwise
dist <- distToNearest(ExampleDb, sequenceColumn="junction",
vCallColumn="v_call_genotyped", jCallColumn="j_call",
model="ham",
first=FALSE, normalize="len",
subsample=30)